Fourier Spectrum:
Any continuous function defined on a finite interval
of length
can be represented as a weighted sum of cosine functions with periods
:
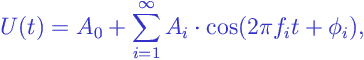 |
where
is the frequency of the i-th Fourier component;
is the amplitude of the i-th component;
is the phase of the i-th component.
The function describing the dependence of the amplitude
on the frequency
in the above expression is called the amplitude spectrum of the function
.
The function describing the dependence of the phase
on the frequency
is called the phase spectrum of the function
.
Thus, the Fourier spectrum of a function is represented by two functions of the frequency
– the amplitude spectrum
and the phase spectrum
. These two are often combined into a single complex-valued function
:
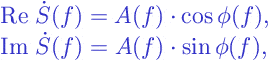 |
where
is the real part of a complex number;
is the imaginable part of a complex number;
The concept of the spectrum plays an important role in signal processing , time series analysis , spectral analysis .
See also: power spectrum .
