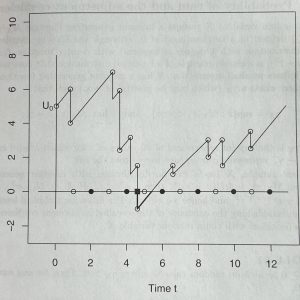
The classic Gambler’s Ruin puzzle has an actuarial parallel: “Ruin Theory,” the calculations that govern what an insurance company should charge in premiums to reduce the probability of “ruin” for a given insurance line. “Ruin” means encountering claims that exhaust initial reserves plus accumulated premiums. The process can be depicted as a time plot, where the y-axis represents net accumulated reserves (increasing gradually as premiums are paid, decreasing sharply with claims paid) and the x-axis represents time. In the illustration below (from Boland, Statistical and Probabilistic Methods in Actuarial Science), ruin happens between times 4 and 5.
A key decision parameter is the “security factor” or “loading factor” on premiums that is set to control the probability of ruin and keep it to a specified level and timing (given assumptions about the frequency and distribution of claims). The calculation can readily be derived from a simulation, although actuarial science has roots going back centuries before the development of computers and, therefore, is heavily oriented to mathematical approaches. Boland’s single chapter on ruin employs most of the English alphabet plus 7 Greek letters in formulas, the Poisson, Cauchy and exponential distributions, the Newton Raphson method, Lundberg’s bound, and one lemma.