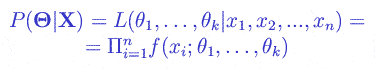Maximum Likelihood Estimator:

The method of maximum likelihood is the most popular method for deriving estimators - the value of the population parameter T maximizing the likelihood function is used as the estimate of this parameter. The general idea behind maximum likelihood estimation is to find the population that is more likely than any other to produce the observed data.

Under mild conditions, the maximum likelihood estimator is asymptotically efficient (see Efficiency, Asymptotic efficiency and asymptotically unbiased. These good properties explain the popularity of the maximum likelihood estimator.

For a random sample of size n, the following general scheme is usually used to derive the maximal likelihood estimator.

Let x₁, x₂, ... , x_n be identically, independently distributed random variables. If the probability density function of the above random variables is , then the likelihood function is defined as

For each sample point X, we wish to find that set of values , denoted by , for which the likelihood function attains its maximum. This , which maximizes the likelihood function given X, is called the maximum likelihood estimator of the parameter .

Browse Other Glossary Entries