Statistical Glossary
Power Mean:
A power mean of order of a set of
values
is defined by the following expression:
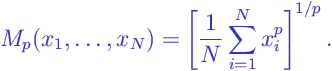 |
The family of power mean statistics is often called the generalized mean – because, for different values of the parameter
, it is equivalent to various types of descriptive statistics:
(i.e
when
) coincides with the arithmetic mean ;
is the harmonic mean ;
is the root mean square .
The greater the parameter , the greater the contribution of the largest values
towards the values of
. If we increase
infinitely, the value of the power mean approaches the maximum value in the sample
, and the reverse – if we decrease
infinitely, then the value of the power mean approaches the minimum value in the sample. This is often denoted as
and
Strictly speaking, is not the arithmetic mean – because this statistic is defined only for non-negative values
, while the arithmetic mean is defined for both negative and non-negative values
).
The power mean is not a “fair” measure of central location – it does not meet requirements of shift invariance , like other statistics defined only for non-negative values (see explanations of central tendency ). Therefore, it would be more correct to classify the power mean as a measure of “average magnitude” or “effective magnitude”. Any power mean
is scale-invariant .
See also Mean values (comparison) and the online short course Basic Concepts in Probability and Statistics
