Statistical Glossary
Scale Invariance (of Measures):
Scale invariance is a property of descriptive statistics . If a statistic is scale-invariant, it has the following property for any sample
and any non-negative value
:
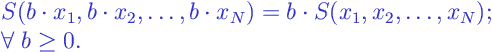 |
(1) |
or, in mathematically equivalent form
In other words, if a statistic is scale-invariant, then multiplication of all elements
of the sample by an arbitrary non-negative value
results in multiplication of the resultant value
of the statistic
by the same value
.
Measures of central tendency and measures of dispersion are normally scale-invariant, as well as most other measures that have values in the same units as the initial data .
Scale invariance is an important practical requirement imposed on many classes of statistical measures. For example, consider data on the selling price of a particular car model at 1000 (
) locations across the country. A market researcher computes the values of two statistics, say,
and
for these data. Statistic
is a measure of central tendency and
is a measure of dispersion. In other words,
reflects a “typical” value of the price, and
reflects the magnitude of variation of the prices
around the typical values. The researcher obtained
and
US dollars. Now, he is asked to report these values in Euro (suppose that 1 dollar = 0.8 Euro). There are two reasonable methods of transition from the initial units (dollars) to new units (euro):
- (i) convert every price
from dollars to Euros – i.e. to multiply it by 0.8 (
), then compute values of the two statistics
and
for the new data
;
- (ii) multiply values of
and
(which are in dollars) by 0.8.
Scale invariance of statistics and
, as defined by expression (1) , guarantees that in both cases the result will be the same.
A general practical recommendation: if a statistic takes on values in the same units as the initial data
, it is strongly recommended to use only scale invariant statistics. Scale invariance of a statistic
may be checked either from analytical considerations or, if this is difficult, at least numerically – by computing values
and
for a few test samples and checking the property (1) .
See also the online short course Basic Concepts in Probability and Statistics
