Uniform Distribution:
The uniform distribution describes probabilistic properties of a continuous random variable that is equally likely to take any value within an interval
, and never takes on values outside this interval.
The uniform distribution is characterised by two parameters – the lower and the upper boundaries of the interval ( and
in our example).
Mathematically, the uniform distribution is described by its probability density described by the following expression:
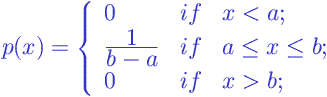 |
The uniform distribution describes, for example, the distribution of errors arising after rounding floating point numbers up to the nearest integer, e.g. in course of analog-to-digit conversion taking place whenever a physical entity, like an image or sound signal, is converted to a digital form.
The uniform distribution is widely used in generation of pseudo-random numbers .
