Statistical Glossary
Weighted Mean:
The weighted mean is a measure of central tendency . The weighted mean of a set of
values
is computed according to the following formula:
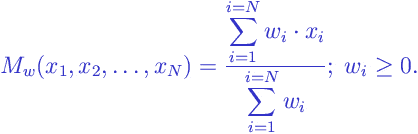 |
where
are non-negative coefficients, called “weights”, that are ascribed to the corresponding values
.
Only the relative values of the weights matter in determining the value of the weighted mean. In other words, if you multiply each weight
by a positive value
and recalculate the weighted mean with new weights
, then the value
remains the same.
The greater the weight in respect to other weights, the greater the contribution of the corresponding datum
into the resultant value
of the weighted mean.
The weighted mean is used, for example, to aggregate a set of scores (e.g. examination scores on different subjects) to a single resultant score. In this case, the magnitude of the weights reflects the importance of their respective subjects. (For this reason, the weighted mean is sometimes named the aggregate mean ).
Besides its use as a descriptive statistic , the weighted mean is also used to construct filters .
See also Mean values (comparison) and the online short course Basic Concepts in Probability and Statistics
