t-distribution:
A continuous distribution, with single peaked probability density symmetrical around the null value and a bell-curve shape. T-distribution is specified completely by one parameter – the number of degrees of freedom.
If X and Y are independent random variables, X has the standard normal distribution and Y – chi-square distribution with N degrees of freedom, then the random variable
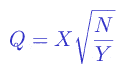
has t-distribution with N degrees of freedom.
It was found by W. S. Gossett, a statistician working for Guiness (the Irish brewery), to be a good approximation to the distribution of the means of randomly drawn samples from a fixed population. Gossett published his findings in 1908 under the name “Student,” hence the distribution is often called the “Student´s t.” In the 1930´s, the t-distribution was also found to be a good approximation to the distribution of the difference in means of two randomly-drawn samples. (Note: the exact distribution of these differences can be derived by permuting the two samples. Before computers, when the derivation of this exact distribution was difficult or impossible to determine, the t-distribution was universally used as a substitute for the exact permutation distribution. With computer intensive methods now widely available, exact tests are increasingly used in preference to the t-distribution.)
See also: t-statistic and t-test
